Inequalities

TODO: inequality # 1. Triangle Inequality The sum of any two sides > the remaining side

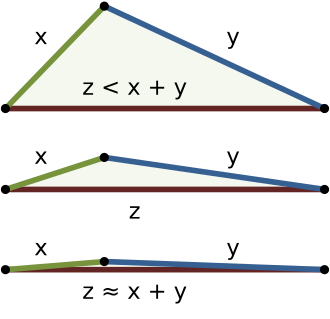
\begin{align} |x+y| \leq |x| + |y| \end{align}

Corollary: \begin{align} ||a| - |b| |\leq |a-b| \\ |a-b| \leq |a| + |b| \end{align} Proof: \begin{align*} &|a| = |a-b+b| \leq |a-b|+|b| \\ &|a| -|b| \leq |a-b| \\ \end{align*}

\begin{align*} &|b| = |b-a+a| \leq |b-a|+|a| \\ &|b|-|a| \leq |b-a| \\ &|a|-|b| \geq -|b-a| \\ \end{align*}

2. Bernoulli’s Inequality

\begin{align} \forall n \in \mathbb{N} , (1+x)^n \leq 1+nx \end{align}

3. Archimedean Property

There not exists a infinitely large real number

\begin{align} \forall x \in \mathbb{R}, \exists n \in \mathbb{N}, x \lt n \end{align}

There not exists a infinitely small positive real number \begin{align} \forall x \gt 0, \exists n \in \mathbb{N}, \frac{1}{n} \lt x \end{align}